Kernel-based Learning: Support Vector Regression

해당 포스트에서는 대표적인 분류 알고리즘 SVM에서 소개된 손실함수를 도입하여 회귀식을 구성하는 SVR(Support Vector Regression) 에 대해 소개하겠습니다. 고려대학교 강필성 교수님의 Business Analytics강의와 김성범 교수님의 Forecasting Model강의를 바탕으로 작성하였습니다.

Regression

회귀 알고리즘은 데이터가 주어졌을 때 데이터를 잘 설명하는 선을 찾고자 합니다. 어떠한 선이 데이터를 잘 설명하는 선이 될까요?

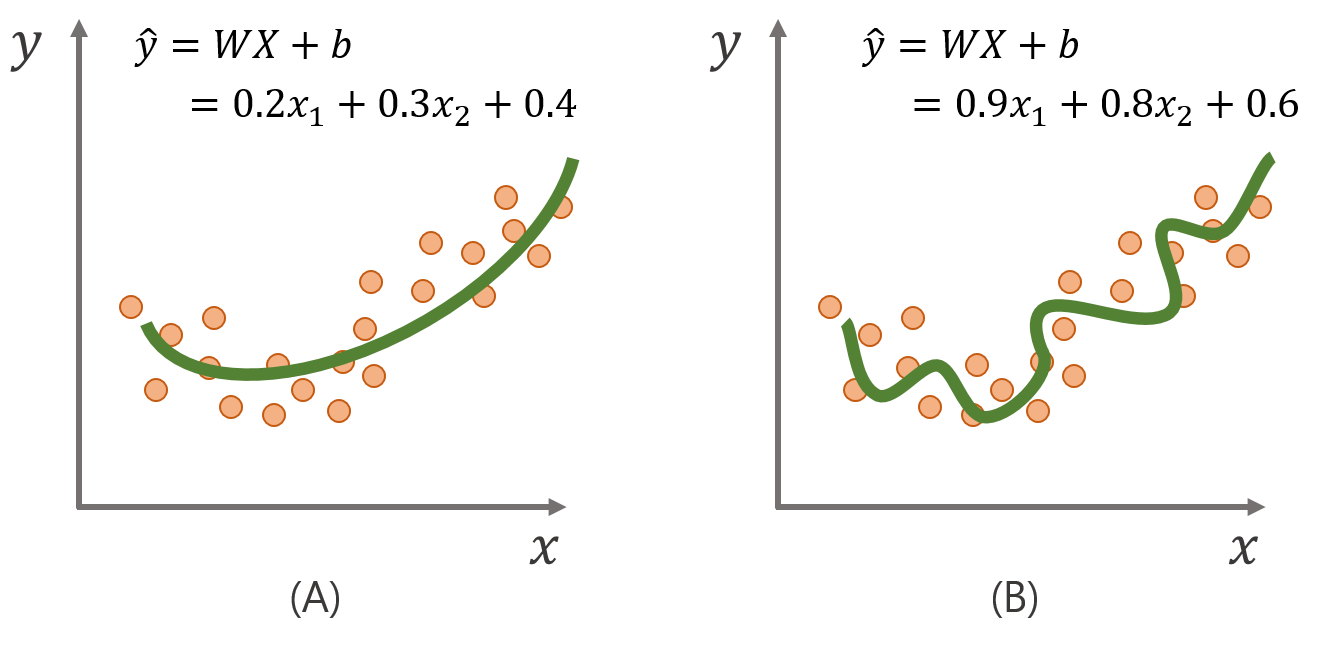
그림(B)의 회귀선은 학습 데이터에는 매우 적합한 회귀선을 구했지만, 새로 들어올 미래 데이터가 조금만 변화하게 되어도 예측 값이 민감하게 변하게 됩니다. 반면 그림(A)에서의 회귀선은 학습데이터의 설명력은 낮아졌지만, 미래 데이터의 변화에 예측 값의 변화가 보다 안정적(robust)입니다.

이처럼 일반 선형회귀 모델에서는 모형이 그림(B)와 같이 과적합(overfitting)하게 되면 회귀 계수 W의 크기도 증가하기 때문에 추가적으로 제약을 부여하여 회귀계수의 크기가 너무 커지지 않도록 penalty식을 부여하여 계수의 크기를 제한하는 정규화(regularized)방법을 적용합니다. 이렇게 penalty식이 추가된 회귀모델은 대표적으로 릿지 회귀모형(Ridge regression)이 있습니다. 릿지 회귀모형의 손실함수 식은 아래와 같이 표현됩니다.

$L_{ridge} = \min \underbrace{\frac { 1 }{ 2 } \sum _{ i=1 }^ n ({ y }_{i} - { f(x_{i}) } )^2}_\text{ loss funciton } + {\lambda} \overbrace{ { \left\| w \right\| }^{ 2} } ^{\text{Robustness}}$

Ridge 손실함수 수식에 담긴 의미를 해석해보면, “실제값과 추정값의 차이를 작도록 하되, 회귀계수 크기가 작도록 고려하는 선을 찾자” 라고 할 수 있습니다.

이러한 릿지 회귀모형은 오늘 포스트의 주제 SVR(Support Vector Regression) 의 목적과 유사합니다. 다만 관점의 차이가 있다면 penalty를 적용시키는 식이 릿지 회귀모형에서의 loss function과 대응되며, 아래와 같이 표현할 수 있습니다.

$L_{SVR} = \min \overbrace { { \left\| w \right\| }^{ 2} } ^{\text {Robustness}}+ {\lambda}\underbrace{ (\frac { 1 }{ 2 } \sum _{ i=1 }^ n {({ y }_{i} - { f(x_{i}) } )^2)}}_\text{ loss funciton }$

SVR 손실함수 수식에 담긴 의미를 해석해보면, “회귀계수 크기를 작게하여 회귀식을 평평하게 만들되, 실제값과 추정값의 차이를 작도록 고려하는 선을 찾자” 라고 할 수 있습니다. 릿지 회귀 모형과 고려사항은 비슷하지만 더 중요하게 생각하는 목적이 다른 셈이죠.

SVR에서 활용할 수 있는 loss function 수식은 매우 다양하며, 앞으로 가장 대표적인 ${\epsilon}$-insensitive함수를 제외한 나머지 함수에 대해서는 ‘비선형 데이터를 활용한 코드 구현 예시’ 파트에서 다뤄보도록 하겠습니다.

Support Vector Regression

1. Original Problem

자, 이제 SVR의 손실함수를 ${\epsilon}$-insensitive함수를 사용한 SVR식으로 표현하겠습니다. 그러자 갑자기 식이 엄청 복잡해 보입니다. 그림을 통해 도대체 ${ \epsilon }$ 와 ${ \xi }$ 가 무엇인지에 대해 알아봅시다.

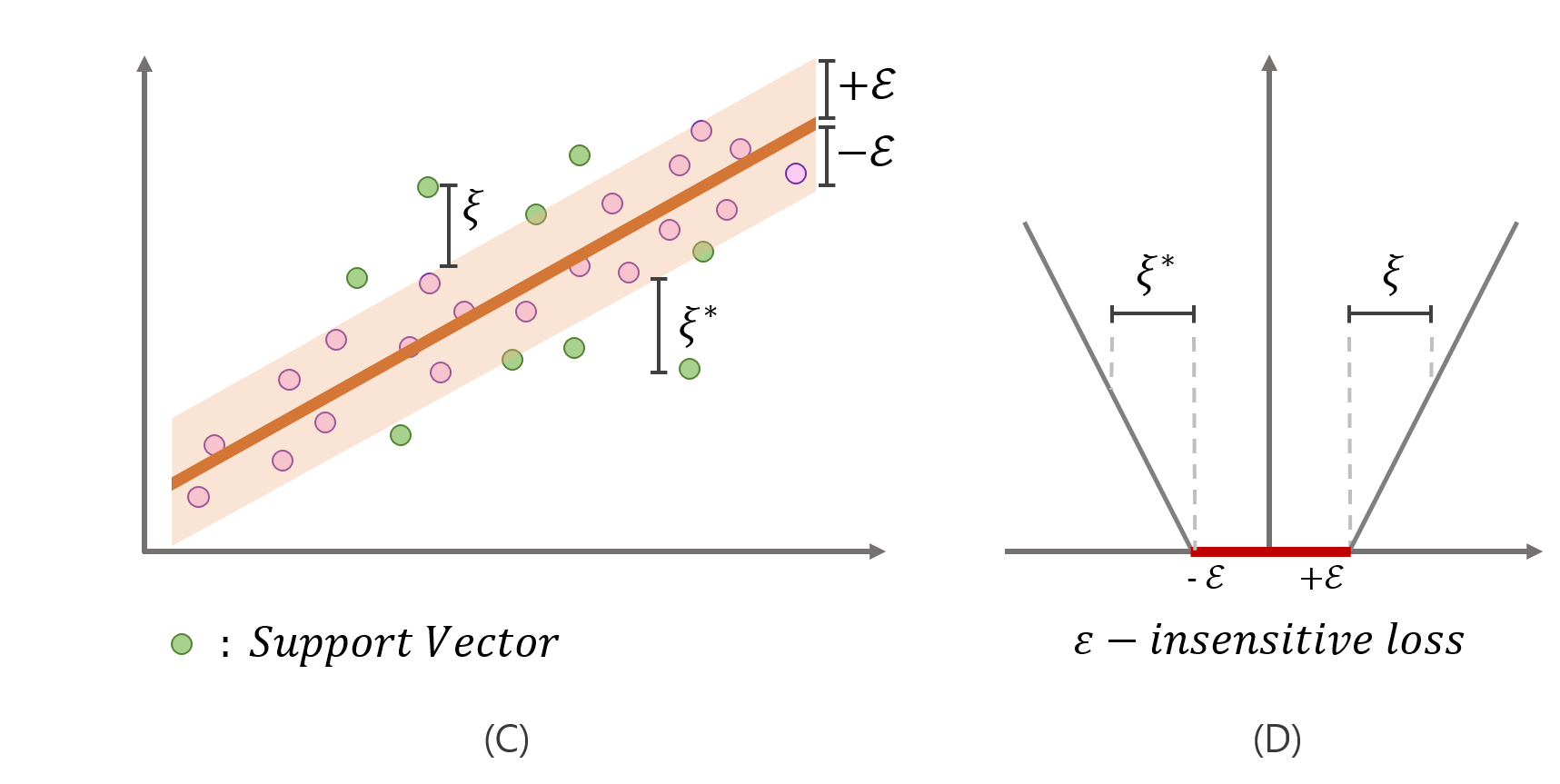
$L_{SVR} =\min \overbrace{ \frac { 1 }{ 2 } { \left\| w \right\| }^{ 2} }^{\text{Robustness}} +C \underbrace{\sum _{ i=1 }^ n {({ \xi }_{ i }+{\xi}_{i}^* )}}_\text{ loss funciton }$ $\\s.t. \quad ({ w }^{ T }{ x }_{ i }+b)-{ y }_{ i }\le {\epsilon}+{ \xi }_{ i }$ $\quad \quad \quad y_i-(w^Tx_i +b) \le {\epsilon}+{ \xi }_i^*$ ${ \xi }_{ i }, { \xi }_{ i }^* \ge {0}$

${ \epsilon }$ : 회귀식 위아래 사용자가 지정한 값 $ \propto $ 허용하는 노이즈 정도
${ \xi }$ : 튜브 밖에 벗어난 거리 (회귀식 위쪽)
${ \xi }^{ * }$ : 튜브 밖에 벗어난 거리 (회귀식 아래쪽)

SVR은 회귀식이 추정되면 회귀식 위아래 2${ \epsilon } (- \epsilon,\epsilon)$만큼 튜브를 생성하여, 오른쪽 그림에서처럼 튜브내에 실제 값이 있다면 예측값과 차이가 있더라도 용인해주기 위해 penalty를 0으로 주고, 튜브 밖에 실제 값이 있다면 C의 배율로 penalty를 부여하게 됩니다. 회귀선에 대해 일종의 상한선, 하한선을 주는 셈이죠. 다시 한 번, SVR의 특징을 정리해보면 다음과 같습니다.

“SVR은 데이터에 노이즈가 있다고 가정하며, 이러한 점을 고려하여 노이즈가 있는 실제 값을 완벽히 추정하는것을 추구하지 않는다. 따라서 적정 범위(2${ \epsilon }$) 내에서는 실제값과 예측값의 차이를 허용한다.”

2. Lagrangian Primal problem

앞서 목적식과 4개의 제약식을 갖춘 original problem을 정의했습니다. 이는 QP(quadratic program)로 바로 최적화 툴을 사용해 풀이할 수 있지만, 4개나 되는 제약식을 모두 만족시키며 푸는 것은 쉽지 않습니다. 따라서 Lagrangian multiplier를 사용하여 제약이 있는 문제를 아래와 같이 제약이 없는 Lagrangian Primal problem으로 변형함으로써 이런 한계를 극복하게 됩니다. 뿐만 아니라 Lagrangian Primal problem은 추후 소개될 커널함수를 사용하기 용이하도록 수식을 재구성하게되는 이점이 있습니다.

${L_{p}} = { \frac { 1 }{ 2 } { \left\| w \right\| }^{ 2} } + C\sum _{ i=1 }^{ n }{ ({ \xi }_{ i }+{\xi}_{i}^* )} - \sum _{ i=1 }^{ n }{ ({ \eta }_{i}{ \xi }_{ i }+{\eta}_{i}^{* }{\xi}_i^* )}$ $\\-\sum _{ i=1 }^{ n }{ { \alpha }_{i}({ \epsilon }+{\xi}_{i}+{y}_{i}-{W}^{T}{x}_{i}-b)} - \sum _{ i=1 }^{ n }{ { \alpha }_{i}^{*}({ \epsilon }+{\xi}_{i}^* -{y}_{i}+{W}^{T}{x}_{i}+b)}$ ${\alpha}_{i}^* ,{\eta}_{i}^* \ge 0$

Lagrangian primal problem으로 재구성한 결과 역시 convex하고, 연속적인 QP(quadratic programming problem)입니다. 이 경우, KKT조건에 의해 목적식의 미지수에 대해 미분 값이 0일때 최적해를 갖게됩니다. 최적해를 찾기위해 목적식의 미지수 $ b, W, { \xi } $ 에 대해 각각 미분해 봅시다.

3. Take a derivative

$\frac { \partial L }{ \partial b }= \boldsymbol{ \sum_{ i=1 }^{ n }{ ({ \alpha }_{ i }-{ \alpha }_{ i }^{ * })} = 0 } \tag{1}$ $\frac { \partial L }{ \partial W }= W - \sum_{ i=1 }^{ n }{ ({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })x_i} = 0 \quad \Rightarrow \quad \boldsymbol{ W = \sum_{ i=1 }^{ n }{ ({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })x_i}} \tag{2}$ $\frac { \partial L }{ \partial \xi^{ * } }= C - { \alpha }_{i}^{ * }-{ \eta }_{ i }^{ * } = 0 \quad \Rightarrow \quad \boldsymbol{ C = { \alpha }_{i}^{ * }-{ \eta }_{ i }^{ * }} \tag{3}$

미지수의 미분 값이 0일때, 3개의 조건(1), (2), (3)을 얻게 됩니다. 이 과정에서 바로 회귀식을 구성는 $ W $와 $ b $ 값이 구해졌다면 좋았을 텐데, Lagrangian multiplier ${\alpha}$값을 모르기 때문에 아직은 바로 구할 수 없습니다. 따라서 미분을 통해 얻은 세가지 조건을 Lagrangian Primal problem 목적식에 다시 대입하여 ${\alpha}$에 대한 식 Lagrangian dual problem으로 새롭게 정리합니다.

4. Lagrangian Dual Problem

${ { L }_{ D } = \frac { 1 }{ 2 } \sum_{ i,j=1 }^{ n }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })({ \alpha }_{ j }^{ * }-{ \alpha }_{ j }) \boldsymbol {x^{T}_{ i }x_{ j }}-{ \epsilon } \sum_{ i,j=1 }^{ n }({ \alpha }_{ i }^{ * }+{ \alpha }_{ i })+\sum_{ i,j=1 }^{ n }y_{ i }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })}$ $s.t. \quad \sum_{ i=1 }^{ n }({ \alpha }_{ i }-{ \alpha }_{ i }^{ * }) = 0 ,\quad{ \alpha }_{ i },{ \alpha }_{ i }^{ * } \in [0,C]$

Lagrangian dual problem으로 재구성한 목적식은 ${\alpha}$로 이루어져있는 convex하고, 연속적인 QP(quadratic programming problem)입니다. 따라서 최적화 툴을 통해 간편하게 ${\alpha}$를 도출할 수 있습니다.

5. Decision function

$\quad W = \sum_{ i=1 }^{ n }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })\boldsymbol x_{ i }\quad \Rightarrow \underbrace{ \quad f(x)=\sum_{ i=1 }^{ n }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })\boldsymbol {x^{T}_{ i }}\boldsymbol {x} + b }_\text{ Regression }$

Lagrangian dual problem을 통해 구한 ${ \alpha }_{ i },{ \alpha }_{ i }^{ * }$ 값을 (2)식에 대입해봅시다. 그러면 우리가 구하고자하는 $W$ 를 구할 수 있게 됩니다. 그렇지만 아직 $b$ 를 구하지 않았기 때문에 회귀식을 구성할 수 없습니다!!

이제 회귀식을 구성하는 마지막 단계인 $b$를 구하는 과정을 봅시다.

$\underbrace{ \quad f(x)=\sum_{ i=1 }^{ n }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })\boldsymbol {x^{T}_{ i }}\boldsymbol {x} + b }_\text{ Regression } \Rightarrow \quad b = f(x) -\sum_{ i=1 }^{ n }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })\boldsymbol {x^{T}_{ i }}\boldsymbol {x} \tag{4}$

$KKT conditions$ 에 의해 다음과 같은 식을 도출할 수 있습니다. (Complementary slackness 조건)

${ \alpha }_{i} ({ \epsilon }+{\xi}_{i} + {y}_{i}-{W}^{T}{x}_{i}-b) = 0 \tag{5}$ ${ \alpha }_{i}^{* }({ \epsilon }+{\xi}_{i }^* -{y}_{i}+{W}^{T}{x}_{i}+b) = 0 \tag{6}$ $(C- { \alpha }_{i}){\xi}_{i } = 0 \tag{7}$ $(C- { \alpha }_{i}^{* }){\xi}_{i }^{* } = 0 \tag{8}$

$b$를 구하기 위해서는 회귀식을 구축하는데 학습하는 데이터 support vector 를 구해야합니다. 식(5)와(7)을사용해서 구해보도록 하겠습니다. 먼저 식(5)에서 ${ \alpha }_{i} { \neq } 0$ 이라면 $({ \epsilon }+{\xi}_{i} + {y}_{i}-{W}^{T}{x}_{i}-b) = 0$ 을 만족해야합니다. 이를 만족한다는 것은 해당 데이터가 튜브 boundary위에 딱 있음을 의미하는데요, 이경우 튜브 밖으로 나간 값이 없으므로 식(7)의 ${\xi}_{i } = 0$ 이라 할 수 있습니다. 그렇게 되면 자연스럽게 $(C- { \alpha }_{i}){ \neq } 0$ 가 성립합니다. 따라서 이경우는 튜브선 위 혹은 그 밖에 있는 데이터를 의미합니다. 반대로 ${ \alpha }_{i}=0$ 이라면, ${\xi}_{i } { \neq } 0$ 라면 $(C- { \alpha }_{i}) = 0$ 이 되어야 합니다. 그렇게 되면 $C = { \alpha }_{i} = 0$ 가 되어 적합하지 않습니다. 식(6),(8)에서도 동일한 결과를 구할 수 있으며 결과적으로 SVR에서의 support vector는 튜브선을 포함하여 바깥쪽에 예측이 된 $x_{sv}$ 입니다.

이제 드디어 $b$를 구할 준비가 끝났습니다. 결론적으로 조건 $0<{ \alpha }_{i} <C$ 혹은 $0<{ \alpha }_{i}^{ * } <C$ 을 충족하는 $x_{sv}$ 만을 (4)식에 대입하게 되면, $b$ 를 구할 수 있게 되는 것이죠. $b$를 구하기 위한 식(4)를 다시 정리하면 다음과 같습니다.

$\quad b = f(x_{sv}) -\sum_{ i=1 }^{ n }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })\boldsymbol {x^{T}_{ i }}\boldsymbol {x}_{sv}$

여기서 support vector의 갯수가 많다면 추정된 $b$ 값의 평균을 구하는 것이 가장 범용적으로 소개된 방법입니다.

자 지금까지 긴 여정을 통해 SVR을 사용한 회귀식에 대해 알아보았습니다. 하지만 지금까지 소개한 SVR 회귀식은 선형성 만을 띄고 있습니다. 하지만 선형성만으로 데이터를 잘 표현하지 못하는 경우가 있기마련입니다. 이런 경우 매핑함수(mapping function)를 사용하여 비선형 문제를 해결할 수 있습니다. 해당 내용을 더욱 자세히 알아봅시다.

6. Support Vector Regression using Kernel function

하단의 그림 (E)와 같이 데이터를 잘 표현하기 위해 비선형 회귀식을 구해야하는 경우 SVR에서는 매핑함수(mapping function)를 사용하여 해결합니다. 매핑 함수는 상대적으로 저차원 데이터 관측치들을 더 높은 차원으로 변환시켜 데이터들을 선형으로 표현가능하게 해보자는 것입니다.

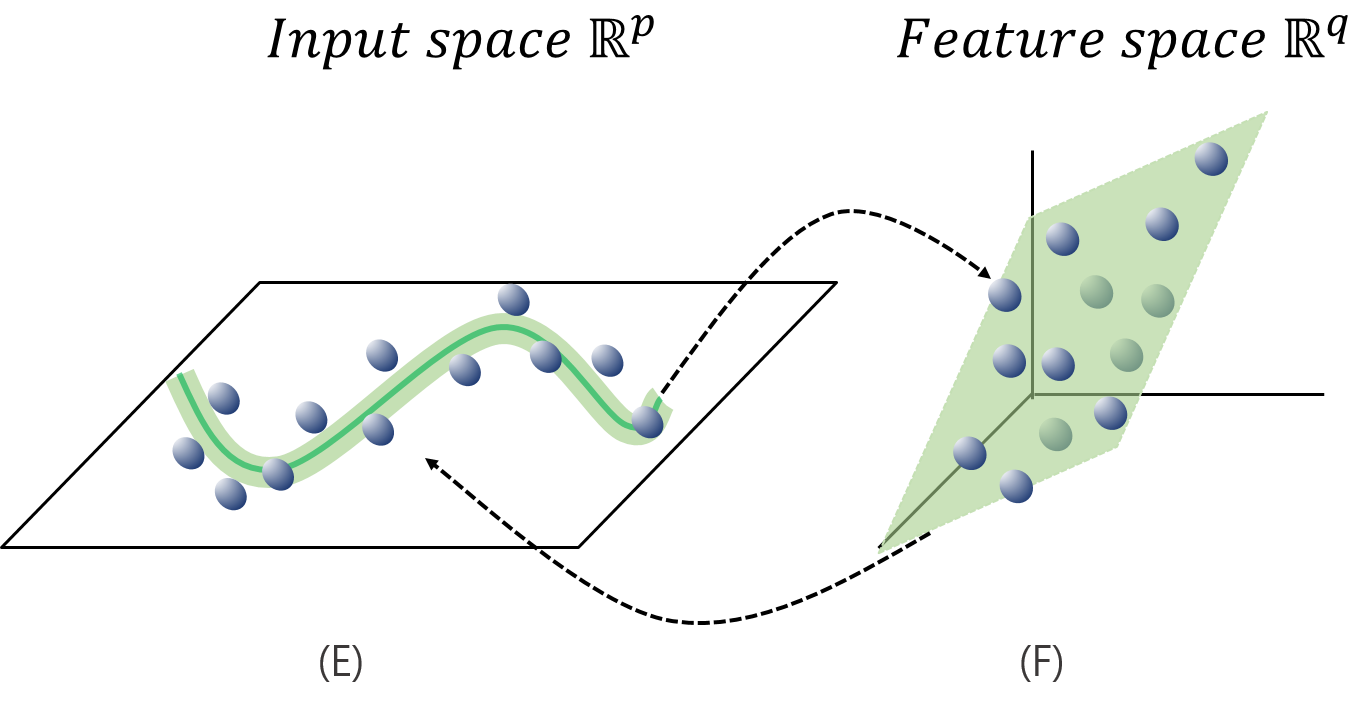
$x = (x_1, x_2, ... x_p) \Rightarrow {\phi}(x) = z = (z_1, z_2, ... x_q)$ $p << q$

결과적으로, 매핑함수를 사용한 SVR의 핵심 내용 정리해보면 다음과 같습니다.

“원공간(Input space)에서의 데이터를 매핑함수 ${\phi}$(x)를 통해 선형으로 구성할 수 있는 고차원 공간(Feature space)로 매핑한 뒤 데이터를 잘 설명하는 선형회귀선을 찾자.”

따라서 선형성을 기반으로 하는 SVR은 원공간이 아닌 고차원공간에서 학습을 시키게 됩니다. 그렇게 되면 결과적으로 비선형성을 띄는 회귀식을 구성할 수 있는 것이죠.

7. Kernel trick

그런데 고차원으로 표현하는 과정은 매우 연산량이 큽니다. 데이터를 고차원으로 매핑하고, 데이터 요소끼리 내적해야하기 때문입니다. 다행히도 SVR은 상대적으로 저차원인 원공간에서 내적을 하고, 고차원공간으로 매핑함으로써 간단히 연산할 수 있는 kernel trick 을 도입했습니다. 따라서 트릭을 가능하게 하는 커널함수(kernel function)을 사용합니다. 따라서 다시 오랜만에 Lagrangian Dual Problem 목적식 으로 돌아가봅시다.

해당 식에서 ${x^{T}_{ i }x_{ j }}$ 에 커널 함수를 사용하여 아래 식과 같이 ${K(x_{ i }x_{ j })}$ 으로 표현하여 고차원 공간으로 변형해줍니다.

8. Dual Lagrangian problem with Kernel trick

${ { L }_{ D } = \frac { 1 }{ 2 } \sum_{ i,j=1 }^{ n }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })({ \alpha }_{ j }^{ * }-{ \alpha }_{ j }) \boldsymbol {K(x_{ i }x_{ j })}-{\epsilon} \sum_{ i,j=1 }^{ n }({ \alpha }_{ i }^{ * }+{ \alpha }_{ i })+\sum_{ i,j=1 }^{ n }y_{ i }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })}$

9. Decision function

$\quad \sum_{ i=1 }^{ n }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })\Phi(\boldsymbol{x_{ i }}) \quad \Rightarrow \quad f(x)=\sum_{ i=1 }^{ n }({ \alpha }_{ i }^{ * }-{ \alpha }_{ i })\boldsymbol{K(x_{ i }x_{ j })} + b$

결과적으로 간편하게 고차원공간으로 매핑하여 다음과 같이 비선형적인 회귀식을 도출할 수 있습니다. 이렇게 커널 트릭으로 활용할 수 있는 커널 함수는 다양하게 있습니다. 대표적으로 RGB, Linear, Polynomial, Sigmoid 등이 있습니다.

비선형 데이터를 활용한 코드 구현 예시

SVR의 경우 고려해야하는 Loss function과 Kernel function, 하이퍼파라미터가 다양하게 존재합니다. 따라서 이들을 변화시키며 결과를 확인해보도록 하겠습니다.

1. 랜덤 데이터 생성

삼각함수를 사용하여 비선형성을 갖는 데이터를 생성하고, 일부 난수에 대해 노이즈를 추가해봅시다.

X = np.sort(10*np.random.rand(100,1), axis=0) # X : 0-10사이 난수를 100개 생성
y = np.sin(X).ravel()                         # y : sin(X)를 통해 비선형 데이터 생성

y[::5] +=2*(0.5-np.random.rand(20))           # 일부 y값에 NOISE 추가
y[::4] +=3*(0.5-np.random.rand(25))
y[::1] +=1*(0.5-np.random.rand(100))

생성된 데이터의 개형은 다음과 같습니다. 데이터들이 sin(X)함수를 기준으로 노이즈가 반영되어 적절히 흩어지게 되었습니다. 해당 데이터를 잘 반영하여 새로운 데이터를 잘 예측하는 회귀선을 구하고자 하는 것이 SVR의 목적이라 할 수 있습니다.

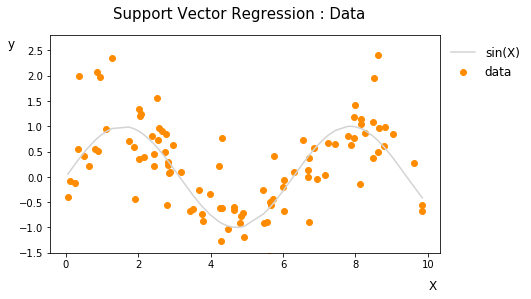
2. Kernel function 비교

Kernel function

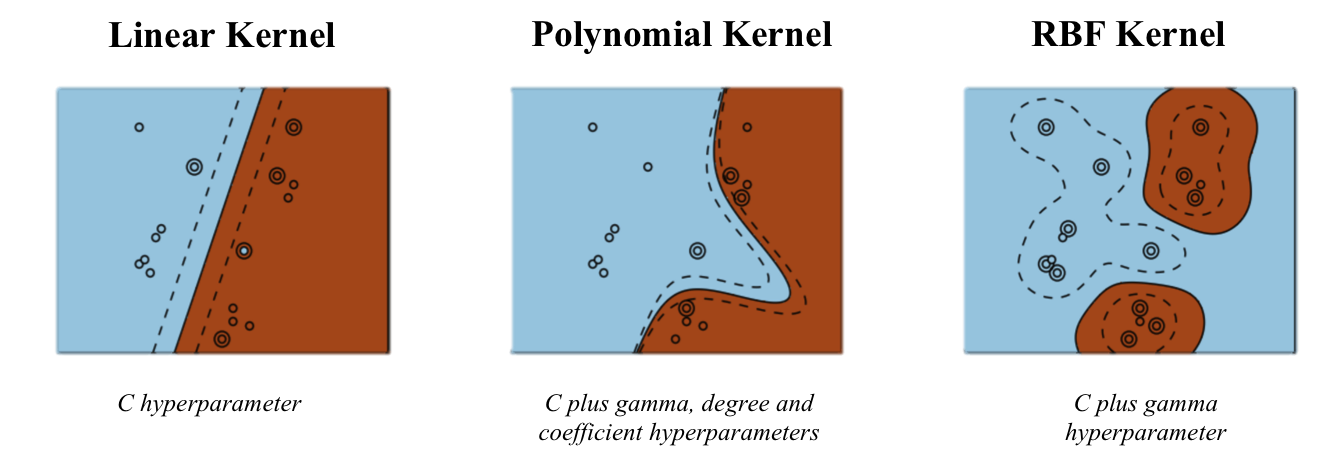
앞서 소개했듯이 대표적인 커널함수(kernel function)는 (1)Linear kernel (2)Polynomial kernel (3)RBF kernel 이 있으며, 이들을 구현한 코드는 다음과 같습니다. 코드 상에서 함수의 하이퍼 파라미터 ‘coef0’는 linear, polynomial, sigmoid kernel에서의 bias값을 의미하며, ‘gamma’는 RBF, sigmoid kernel에서 $1/\sigma^2$을 의미합니다. ‘gamma’로 치환하므로써 연산을 보다 용이하게 개선할 수 있습니다.

def kernel_f(xi, xj, kernel = None, coef0=1.0, degree=3, gamma=0.1):

    if kernel == 'linear':                                  # Linear kernel
        result = np.dot(xi,xj)+coef0
    elif kernel == 'poly':                                  # Polynomial kernel
        result = (np.dot(xi,xj)+coef0)**degree
    elif kernel == 'rbf':                                   # RBF kernel
        result = np.exp(-gamma*np.linalg.norm(xi-xj)**2)
    elif kernel =='sigmoid':                                # Sigmoid kernel
        result = np.tanh(gamma*np.dot(xi,xj)+coef0)
    else:                                                   # Dot product
        result = np.dot(xi,xj)

    return result

Kernel matrix

두 원소값에 대한 스칼라 $K(x_i,x_j)$를 구할 수 있으며, 모든 원소간(Pair-wise) $K$값을 구해 Kernel matrix(Gram matrix)를 도출해야합니다. 최종적으로 도출되는 커널행렬(Kernel matrix)은 대칭행렬(Symmetric matrix) 이고, 모든 $K$값이 양수인 Positive semi-definite 행렬 이라는 특징을 갖고있습니다. 아래 코드를 통해 앞서 정의한 커널함수에 따른 커널행렬을 구합니다.

def kernel_matrix(X, kernel, coef0=1.0, degree=3, gamma=0.1):

    X = np.array(X,dtype=np.float64)
    mat = []
    for i in X:
        row = []
        for j in X:
            if kernel=='linear':           
                row.append(kernel_f(i, j, kernel = 'linear', coef0))   
            elif kernel=='poly':
                row.append(kernel_f(i, j, kernel = 'poly', coef0, degree))
            elif kernel=='rbf':
                row.append(kernel_f(i,j,kernel = 'rbf', gamma))
            elif kernel =='sigmoid':
                row.append(kernel_f(i,j,kernel = 'sigmoid', coef0, gamma))    
            else:
                row.append(np.dot(i,j))
        mat.append(row)

    return mat

커널함수만을 변형시켜 회귀계수 추정을 비교해봅시다. 커널함수비교를 위해 손실함수는 epsilon insensitive로, 하이퍼 파라미터는 (epsilon=1, C=0.001, gamma=0.1)로 정의했습니다. 한눈에 보기에도 해당 데이터에는 RBF kernel 을 사용한 회귀분석이 가장 적합한 것을 확인할 수 있었습니다. 이처럼 주어진 데이터에 사용하는 커널함수에 따라 feature space의 특징이 달라지기 때문에 데이터 특성에 적합한 커널함수를 결정하는 것은 중요합니다.

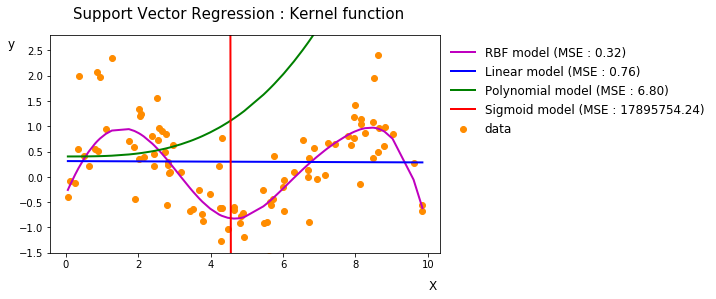
생성 데이터에 적합한 커널함수는 test set의 MSE가 가장 낮은 RBF kernel function이라 할 수 있겠습니다. 그래프를 봐도 가장 적합하게 예측하는게 보이죠.

3. Loss function 비교

Loss function

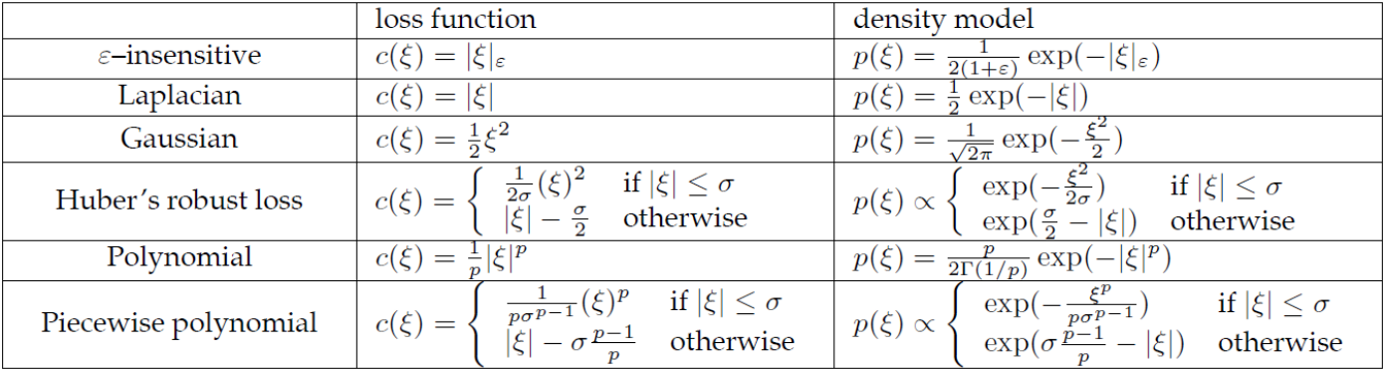
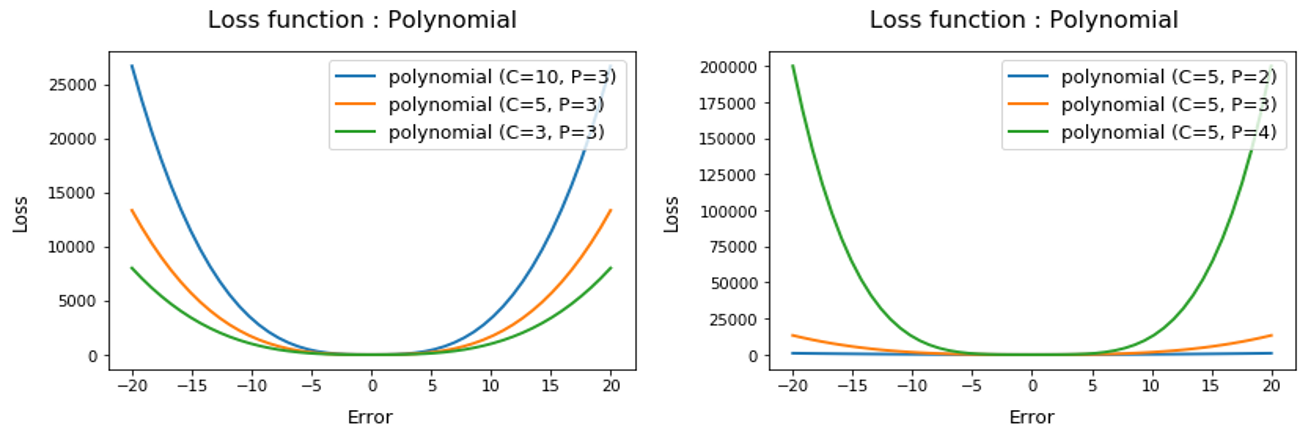
앞서 이론설명에서 말했듯, SVR은 ${\epsilon}$-insensitive함수를 제외하고도 다양한 손실함수로 변형하여 사용할 수 있습니다. 익숙한 Gaussian, Polynomial 이외에도 다양한 함수가 존재함을 확인할 수 있습니다. 특히 piecewise polynomial의 경우 ${\sigma}$ 를 경계로 penalty값이 확 오르는게 신기합니다.

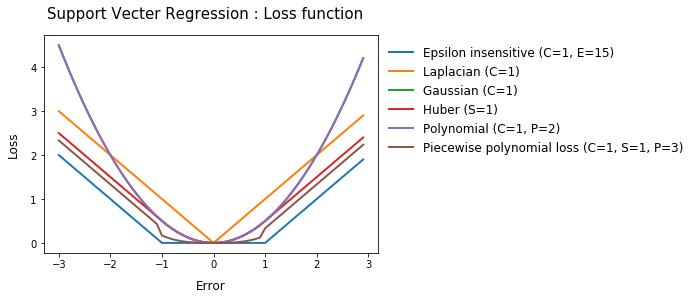
Loss function hyper parameter

각 손실함수를 구현하는 코드와 함께 손실함수의 파라미터 변화에 따라 loss값의 개형이 어떻게 변하는지 각각 비교해봅시다. 코드 및 그래프에서 하이퍼파라미터는 다음과 같습니다. C : cost , E : epsilon , P : degree , S : ${\sigma}$

${\epsilon}$-insensitive loss function

## Epsilon - insensitive loss
def eps_loss(t, c=3, e = 5):
    return(abs(t)<e)*0* abs(t) +((t)>=e)*c*abs(t-e) +((t)<-e)*c*abs(t+e)

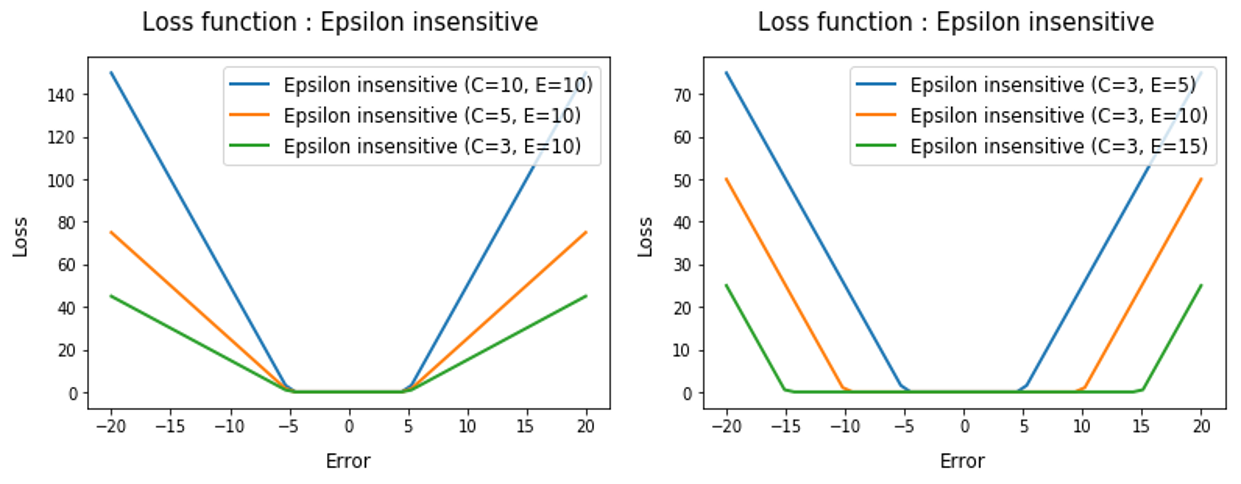
Laplacian loss function

## Laplacian loss
def laplacian_loss(t, c=3):
    return c*abs(t)

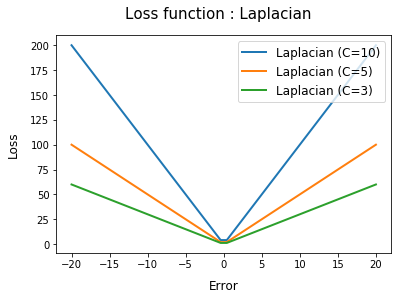
Gaussian loss function

## Gaussian loss
def gaussian_loss(t, c=3):
    return c*0.5*t**2    

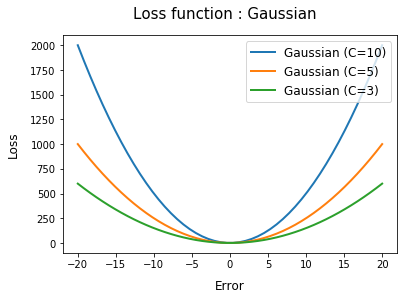
Huber loss function

## Hubor loss
def huber_loss(t, c=3, s=5):
    return c*((abs(t)<s)*(0.5/s)*(t**2) + (abs(t)>=s)*(abs(t)-s/2))

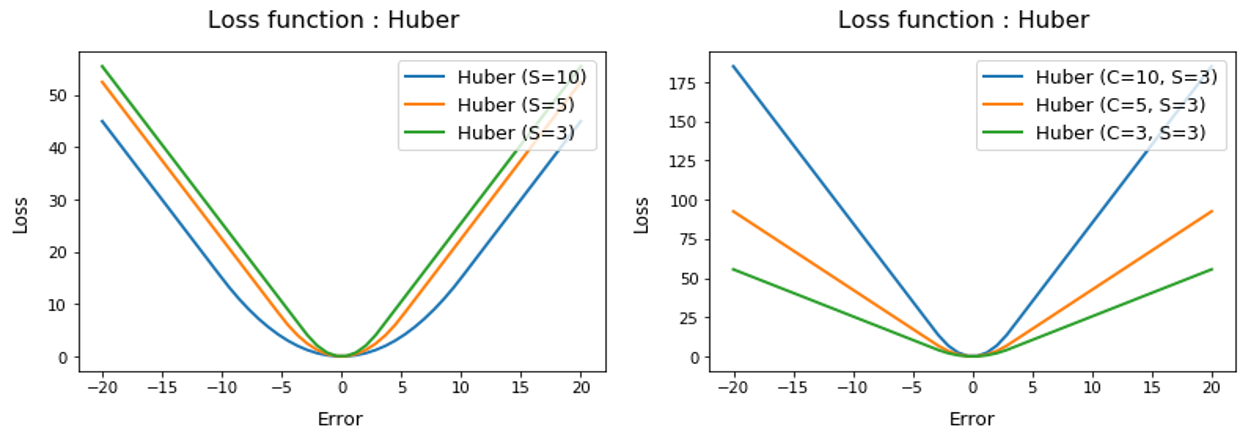
Polynomial loss function

# Polynomial loss
def poly_loss(t, c=3, p=3):
    return c*((p**-1)*abs(t)**p)

Piecewise loss function

## Piecewise polynomial
def Picewise_polynomial_loss(t, c=3, s=5, p=3):
    return c*((abs(t)<=s)*((abs(t)**p)/p/(s*(p-1)))+(abs(t)>s)*(abs(t)-(s*(p-1))/p))  

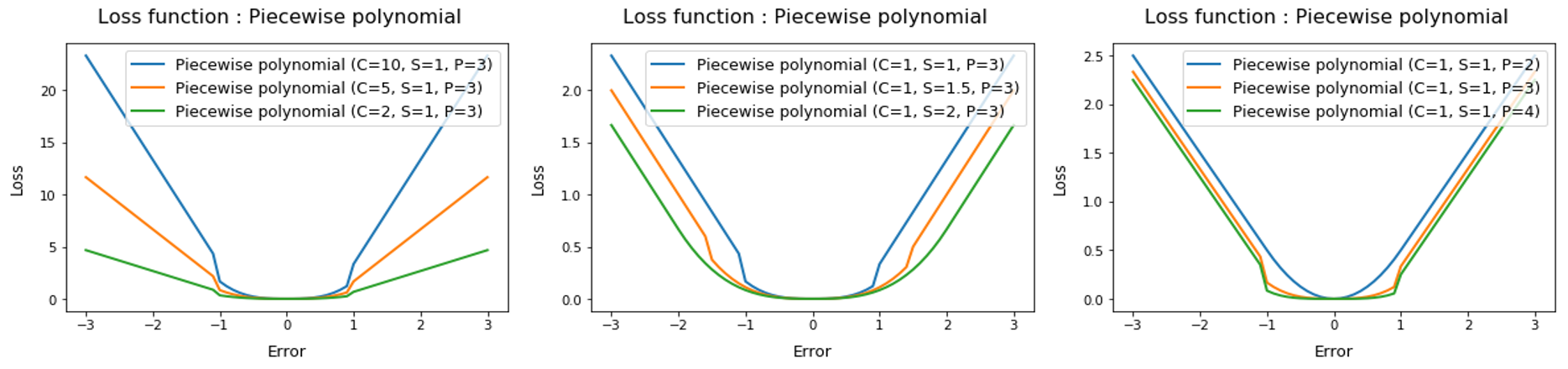
이전에 생성한 랜덤데이터에는 어떤 loss function이 가장 MSE기준으로 좋은 성능을 보이는지 확인해봅시다. 아래 그래프에서 확인할 수 있듯이 ${\epsilon}$-insensitive 손실함수 가 가장 좋은 성능을 보임을 확인할 수 있었습니다. 이 때 최적화 solver로 풀이가능하도록 코드를 각 손실함수들을 quadratic형으로 변환하여 작성해야합니다. 해당 코드는 포스트 뒤에 Appendix에서 다루도록 하겠습니다.

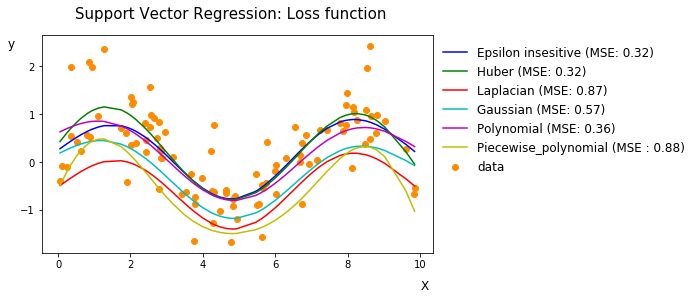
${\epsilon}$-insensitive Hyper parameter

생성 데이터에 대해 RBF kernel 과 ${\epsilon}$-insensitive 손실함수 로 모델을 구성한 경우 성능이 좋은 것을 확인할 수 있었습니다. ${\epsilon}$-insensitive 손실함수의 다양한 하이퍼파라미터를 변경하게될 때에는 결과값이 어떻게 바뀌게 될까요? 하이퍼파라미터 C(cost), epsilon, gamma를 바꾸어가며 비교해봅시다.

$L_{SVR} = \min \overbrace { { \left\| w \right\| }^{ 2} } ^{\text {Robustness}}+ {\lambda}\underbrace{ (\frac { 1 }{ 2 } \sum _{ i=1 }^ n {({ y }_{i} - { f(x_{i}) } )^2)}}_\text{ loss funciton }$

Cost 변경 [ 1,0.3,0.1,1e-06 ] ( Epsilon = 0.2 , gamma = 0.1 )

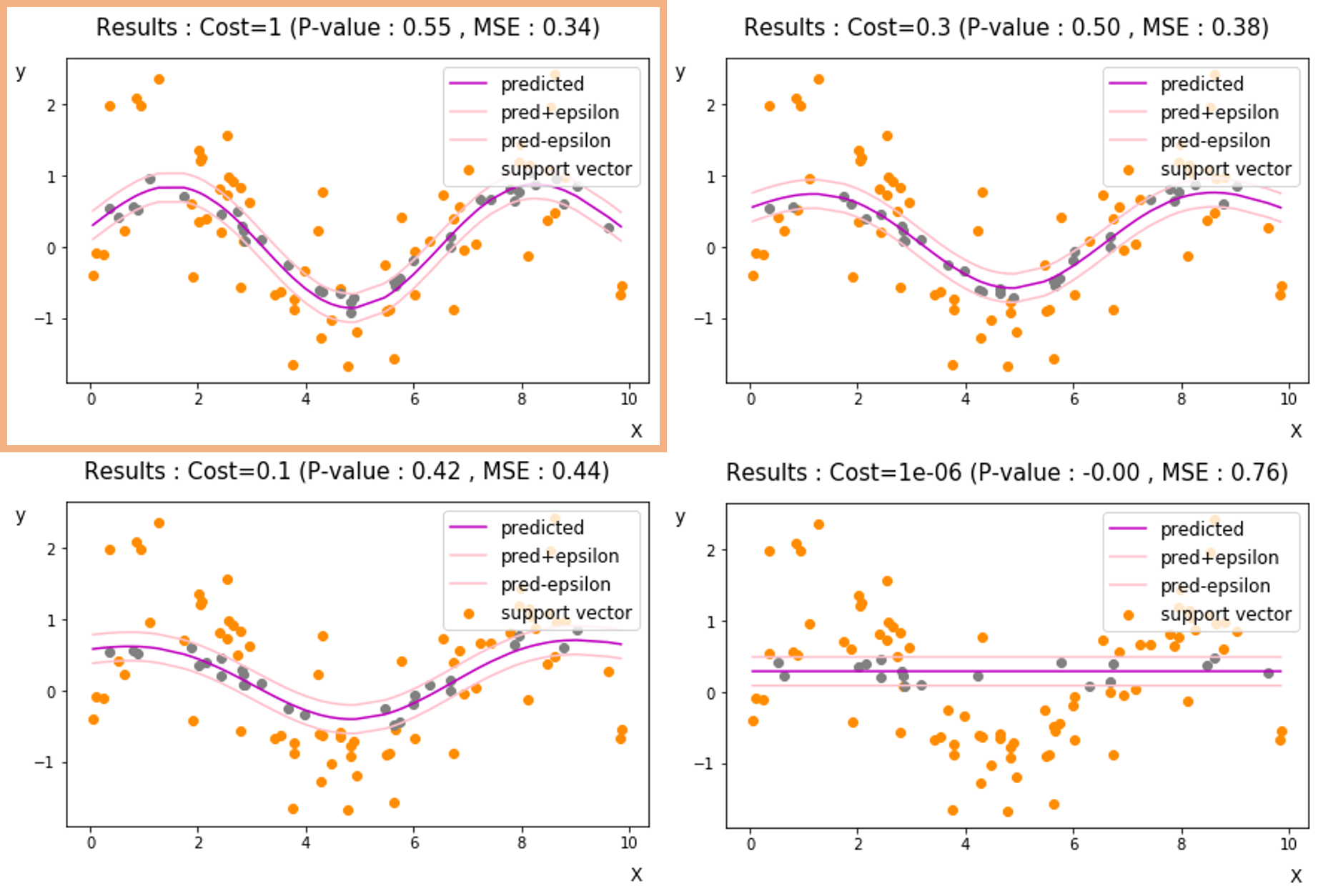
Cost는 작아질수록 잘못 예측된 값에 대해 penalty부여를 적게 하기 때문에 실제값과의 차이가 중요하지 않게됩니다. 따라서 회귀계수를 줄이고자하는 $\overbrace { { \left\| w \right\| }^{ 2} } ^{\text {Robustness}}$ 식을 더 비중있게 다루게 됩니다. 따라서 회귀식이 평평해지는 것을 확인할 수 있으며, 예측성능 또한 감소한것을 볼 수 있습니다.

Epsilon 변경 [ 0.2, 0.6, 1.4, 1.8 ] ( Cost = 1 , gamma = 0.1 )

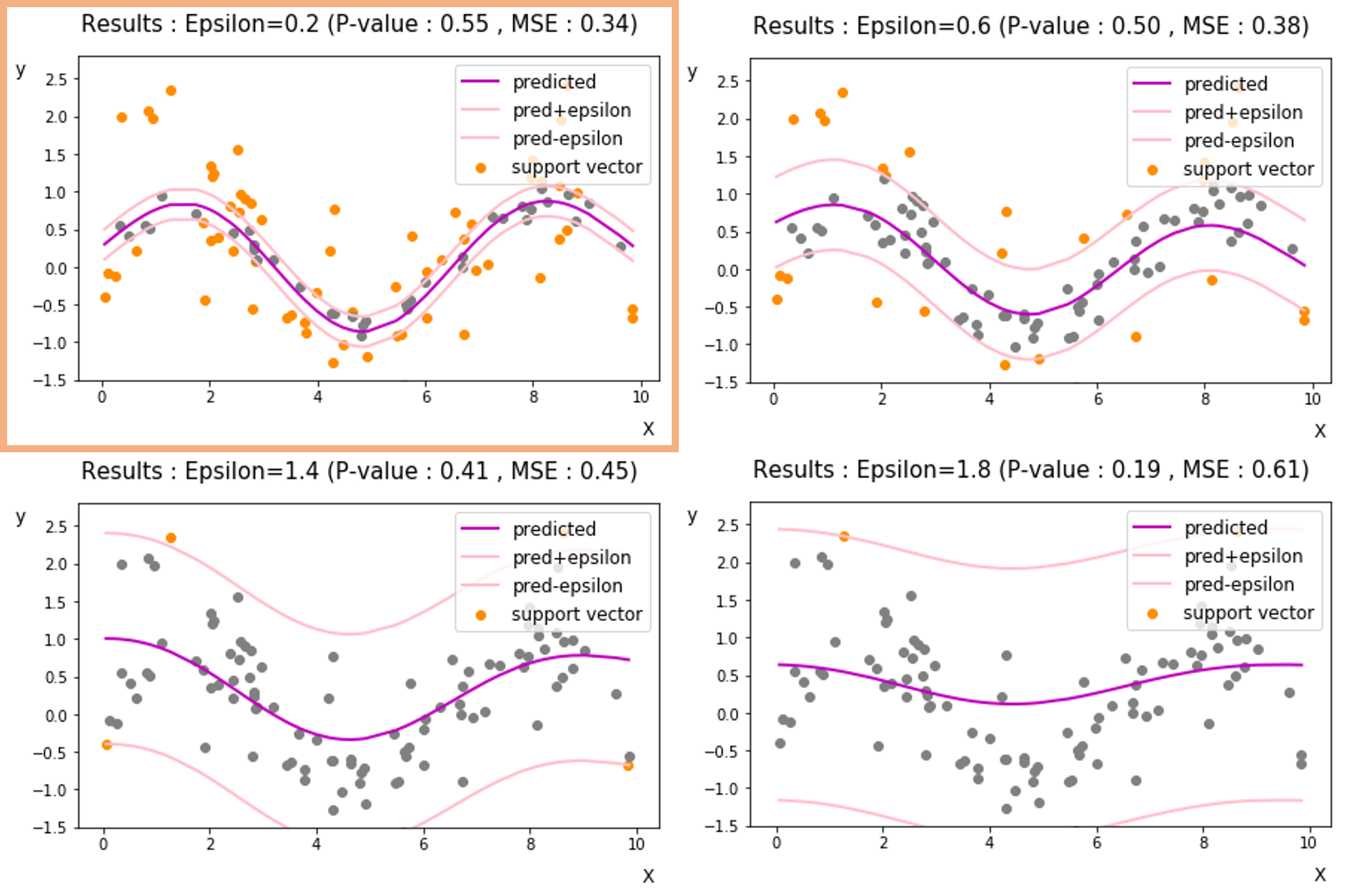
${\epsilon}$을 키우게 되면, 더 큰 구간 $2{\epsilon}$ 내에서 penalty를 부여하지 않게됩니다. 즉, 노이즈로 인식하고 맞춘셈 치는 값들이 많아지는 것이죠. 결과적으로 회귀식을 구성하는 support vector의 수도 감소하게 되고, 평평한 회귀식을 구상할 수 있게됩니다.

Gamma 변경 [ 0.1, 0.7, 1, 5 ] ( Epsilon = 0.2, Cost = 1 )

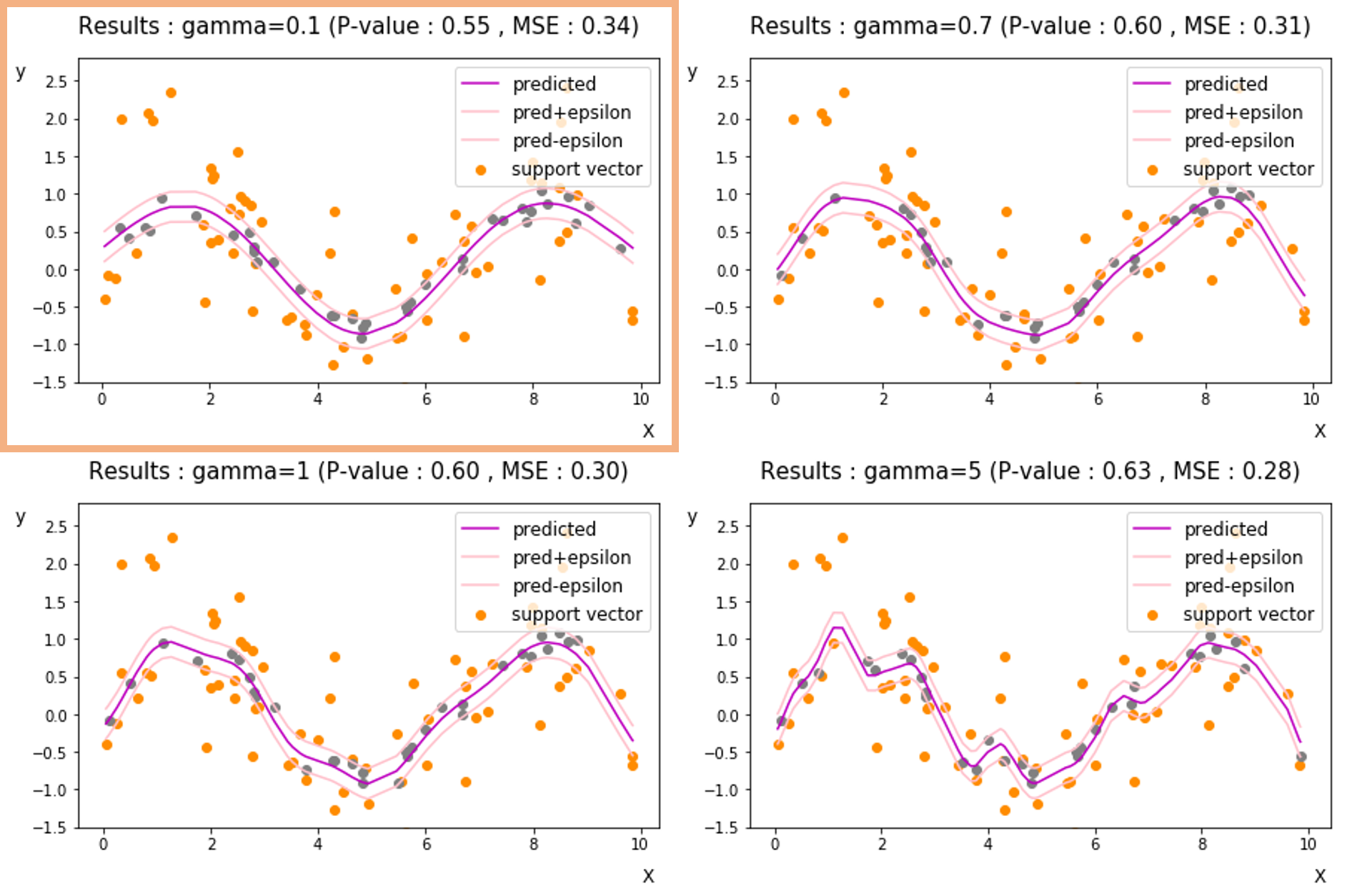
gamma의 경우 RBF커널함수에서 $\frac { 1 }{ \sigma^{2} }$ 과 같은 의미이지만, 계산의 용의성을 위해 다르게 표현한 것입니다. gamma는 커널의 폭을 제어하게되는데요, gamma가 클수록 회귀선이 꼬불꼬불해지는 것을 확인할 수 있습니다.

해당 포스트를 통해 SVR의 개념과 수식전개를 비롯해 코드로 구현하는 과정에 대해 알아보았습니다. 또한 구현 과정에서 하이퍼파라미터를 다양하게 설정하고, 변화에 따른 회귀선의 변화가 어떻게 진행되는지 가시적으로 확인할 수 있었습니다.

Appendix : 손실함수들을 quadratic형으로 변환하여 Class로 정의

## Quadratic form
class svr:
    '''
    loss: ['epsilon-insensitive','huber','laplacian','gaussian','polynomial','piecewise_polynomial'] defualt: epsilon-insensitive
    kernel: [None,'rbf', 'linear','poly']
    coef0: Independent term in kernel function. in 'linear','poly'
    degree: Degree of the polynomial kernel function (‘poly’). Ignored by all other kernels.
    gamma: Kernel coefficient for ‘rbf’, ‘poly’
    p: polynomial/'piecewise_polynomial loss function p
    sigma: for loss function
    '''
    def __init__(self,loss = 'epsilon-insensitive',C = 1.0, epsilon = 1.0,
                 kernel = None, coef0=1.0, degree=3, gamma=0.1, p=3, sigma=0.1):
        self.loss = loss
        self.kernel = kernel
        self.C = C
        self.epsilon = epsilon
        self.coef0 = coef0
        self.degree= degree
        self.gamma = gamma
        self.sigma = sigma
        self.p = p

    #model fitting    
    def fit(self,X,y):
        self.X = X
        self.y = y

        n = self.X.shape[0]#numper of instances
        #variable for dual optimization problem

        alpha = cvx.Variable(n)
        alpha_ = cvx.Variable(n)
        one_vec = np.ones(n)

        #object function and constraints of all types of loss fuction

        if self.loss == 'huber':
            self.constraints = []
            self.svr_obj = cvx.Maximize(-.5*cvx.quad_form(alpha-alpha_, kernel_matrix(self.X,kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma)) - self.epsilon*one_vec*(alpha+alpha_) + self.y*(alpha-alpha_) - self.sigma/(2*self.C)*one_vec*(cvx.power(alpha, 2) + cvx.power(alpha_, 2)))
            self.constraints += [cvx.sum(one_vec*alpha - one_vec*alpha_) == 0]
            for i in range(n):
                self.constraints += [alpha[i] >= 0, alpha_[i] >=0]
            svr = cvx.Problem(self.svr_obj,self.constraints)
            svr.solve()

            #alpha & alpha_
            self.a = np.array(alpha.value).flatten()
            self.a_ = np.array(alpha_.value).flatten()

            #compute b
            idx = np.where((np.array(alpha.value).ravel() < self.C-1E-10) * (np.array(alpha.value).ravel() > 1E-10))[0][0]
            self.b = -self.epsilon + self.y[idx] - np.sum([(alpha.value[i]-alpha_.value[i])*kernel_f(self.X[idx], self.X[i],
                                       kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma) for i in range(n)])

        elif self.loss == 'laplacian': # epsilon = 0 of epsilon-insensitive
            self.constraints = []
            self.svr_obj = cvx.Maximize(-.5*cvx.quad_form(alpha-alpha_,
                                                     kernel_matrix(self.X,kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma)) + self.y*(alpha-alpha_))
            self.constraints += [cvx.sum(one_vec*alpha - one_vec*alpha_) == 0]
            for i in range(n):
                self.constraints += [alpha[i] >= 0, alpha_[i] >=0, alpha[i] <= self.C, alpha_[i] <= self.C]
            svr = cvx.Problem(self.svr_obj,self.constraints)
            svr.solve()

            #alpha & alpha_
            self.a = np.array(alpha.value).flatten()
            self.a_ = np.array(alpha_.value).flatten()

            #compute b
            idx = np.where((np.array(alpha.value).ravel() < self.C-1E-10) * (np.array(alpha.value).ravel() > 1E-10))[0][0]
            self.b = -self.epsilon + self.y[idx] - np.sum([(alpha.value[i]-alpha_.value[i])*kernel_f(self.X[idx], self.X[i],
                                       kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma) for i in range(n)])

        elif self.loss == 'gaussian': # sigma = 1 of huber
            self.constraints = []
            self.svr_obj = cvx.Maximize(-.5*cvx.quad_form(alpha-alpha_,
                                                     kernel_matrix(self.X,kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma)) - self.epsilon*one_vec*(alpha+alpha_) + self.y*(alpha-alpha_) - 1./(2*self.C)*one_vec*(cvx.power(alpha, 2) + cvx.power(alpha_, 2)))
            self.constraints += [cvx.sum(one_vec*alpha - one_vec*alpha_) == 0]
            for i in range(n):
                self.constraints += [alpha[i] >= 0, alpha_[i] >=0]
            svr = cvx.Problem(self.svr_obj,self.constraints)
            svr.solve()

            #alpha & alpha_
            self.a = np.array(alpha.value).flatten()
            self.a_ = np.array(alpha_.value).flatten()

            #compute b
            idx = np.where((np.array(alpha.value).ravel() < self.C-1E-10) * (np.array(alpha.value).ravel() > 1E-10))[0][0]
            self.b = -self.epsilon + self.y[idx] - np.sum([(alpha.value[i]-alpha_.value[i])*kernel_f(self.X[idx], self.X[i],
                                       kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma) for i in range(n)])

        elif self.loss == 'polynomial':
            self.constraints = []
            self.svr_obj = cvx.Maximize(-.5*cvx.quad_form(alpha-alpha_,
                                                     kernel_matrix(self.X,kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma)) + self.y*(alpha-alpha_) - (self.p-1)/(self.p*self.C**(self.p-1))* one_vec*(cvx.power(alpha, self.p/(self.p-1)) + cvx.power(alpha_, self.p/(self.p-1))))
            self.constraints += [cvx.sum(one_vec*alpha - one_vec*alpha_) == 0]
            for i in range(n):
                self.constraints += [alpha[i] >= 0, alpha_[i] >=0]
            svr = cvx.Problem(self.svr_obj,self.constraints)
            svr.solve()

            #alpha & alpha_
            self.a = np.array(alpha.value).flatten()
            self.a_ = np.array(alpha_.value).flatten()

            #compute b
            idx = np.where((np.array(alpha.value).ravel() < self.C-1E-10) * (np.array(alpha.value).ravel() > 1E-10))[0][0]
            self.b = -self.epsilon + self.y[idx] - np.sum([(alpha.value[i]-alpha_.value[i])*kernel_f(self.X[idx], self.X[i],
                                       kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma) for i in range(n)])

        elif self.loss == 'piecewise_polynomial':
            self.constraints = []
            self.svr_obj = cvx.Maximize(-.5*cvx.quad_form(alpha-alpha_,
                                                     kernel_matrix(self.X,kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma)) + self.y*(alpha-alpha_) - (self.p-1)*self.sigma/(self.p*self.C**(self.p-1))* one_vec*(cvx.power(alpha, self.p/(self.p-1)) + cvx.power(alpha_, self.p/(self.p-1))))
            self.constraints += [cvx.sum(one_vec*alpha - one_vec*alpha_) == 0]
            for i in range(n):
                self.constraints += [alpha[i] >= 0, alpha_[i] >=0]
            svr = cvx.Problem(self.svr_obj,self.constraints)
            svr.solve()

            #alpha & alpha_
            self.a = np.array(alpha.value).flatten()
            self.a_ = np.array(alpha_.value).flatten()

            #compute b
            idx = np.where((np.array(alpha.value).ravel() < self.C-1E-10) * (np.array(alpha.value).ravel() > 1E-10))[0][0]
            self.b = -self.epsilon + self.y[idx] - np.sum([(alpha.value[i]-alpha_.value[i])*kernel_f(self.X[idx], self.X[i],
                                       kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma) for i in range(n)])
        else:
            self.constraints = []
            self.svr_obj = cvx.Maximize(-.5*cvx.quad_form(alpha-alpha_, kernel_matrix(self.X,kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma)) - self.epsilon*one_vec*(alpha+alpha_) + self.y*(alpha-alpha_))
            self.constraints += [cvx.sum(one_vec*alpha - one_vec*alpha_) == 0]
            for i in range(n):
                self.constraints += [alpha[i] >= 0, alpha_[i] >=0, alpha[i] <= self.C, alpha_[i] <= self.C]
            svr = cvx.Problem(self.svr_obj,self.constraints)
            svr.solve()

            #alpha & alpha_
            self.a = np.array(alpha.value).flatten()
            self.a_ = np.array(alpha_.value).flatten()

            #compute b
            idx = np.where((np.array(alpha.value).ravel() < self.C-1E-10) * (np.array(alpha.value).ravel() > 1E-10))[0][0]
            self.b = -self.epsilon + self.y[idx] - np.sum([(alpha.value[i]-alpha_.value[i])*kernel_f(self.X[idx], self.X[i],
                                       kernel=self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma) for i in range(n)])


    def predict(self,new_X):
        self.results = []
        n = new_X.shape[0]
        for j in range(n):
            X = new_X[j]
            self.results += [np.sum([(self.a[i] - self.a_[i]) *kernel_f(X, self.X[i],
                                     kernel = self.kernel,coef0=self.coef0,degree=self.degree,gamma=self.gamma) for i in range(n)]) + self.b]   
        return self.results